Algorithm for knight’s tour in Python

I’ve written an updated version of this code here. Please take a look! It adds a visualizer, ability to solve for closed tours and step requirements, and has a better exiting strategy. 🙂

---

In Discrete class, we’ve been talking about planar graphs and stuff like Hamilton traversals. One of our in-class exercises involved the knight’s tour, and whether we could find a rule that would allow us to decided if a knight’s tour was possible given a chessboard of a certain dimension. I have a hard time understanding graphs, but the “Knight’s Tour” sounded really cool so I looked it up on Wikipedia. The problem is actually a pretty interesting one, so I decided to try my hand at implementing an algorithm for solving it in Python.

From Wikipedia:
A knight’s tour is a sequence of moves of a knight on a chessboard such that the knight visits every square only once. If the knight ends on a square that is one knight’s move from the beginning square (so that it could tour the board again immediately, following the same path), the tour is closed, otherwise it is open.

The .gif below is an example of what knight’s tour would look like on an 8×8 board.

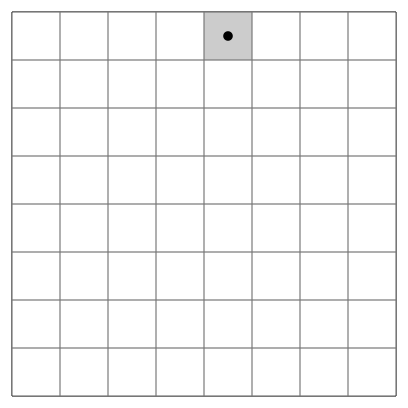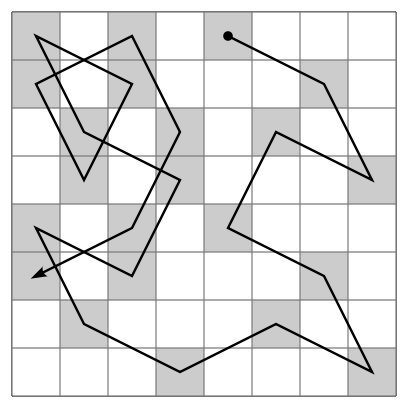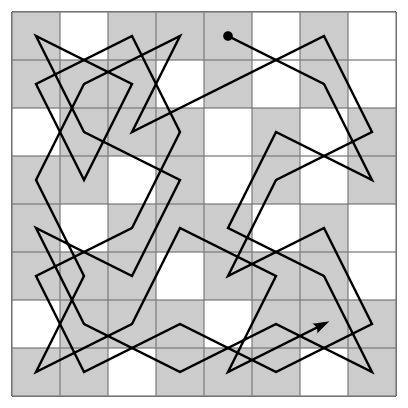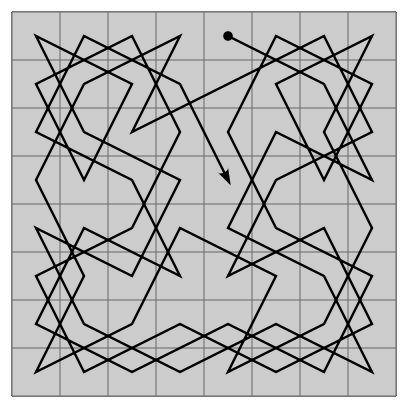
In writing my own implementation, I heavily referenced this site and this site. I’ll do a walkthrough of my code below.

It makes the most sense to use a depth-first-search in our implementation, because the solution to the problem is quite far from the root since the it (the solution) has exactly M*N – 1 moves. (Where M and N are the dimensions of the board.)

I represent the chessboard as a list of lists, only because its easy that way. The position of a chessboard is indexed like so:

self.board[m][n]

Where m is the Y location and n is the X location.

During each step of the tour, the algorithm will find all of the next valid moves, and recursively run self.tour() with updated n (count), path (currently traversed points from the starting point), and to_visit (next point to visit) variables. This recursive call will continue until the function reaches a dead end where no more valid moves can be made, in which case it’ll backtrack to the last move made and try again with a different to_visit value.

An optimization was made in the form of self.sort_lonely_neighbors(), by observing the Warnsdorf’s rule heuristic. The heuristic works as follows: The knight will choose his next move by moving to a square that has the fewest next possible moves. By sorting the nodes to visit by how many possible moves are next, our knight will always traverse the graph from the edges in. This sort of logic makes sense, because it’s much easier to visit an empty square on the edge of a chessboard near the beginning of the tour without getting trapped than later on.

By default the script starts at position (0,0) on an 8×8 chessboard. However, it can be easily modified. It solved a 31×31 chessboard in less than a second, which I am mighty proud of. When I tried to go to a 50×50 chessboard, I got recursion depth exceeded errors… which I wonder if I could get around by doing something a bit more complicated than a simple recursive program. Hmm… Interesting problem for another day I guess!